忆阻器（一）——基本概念和实例

忆阻器字面包含两层意思：一是电阻，二是具有记忆性。它是伯克利的蔡少棠教授从电路完备性角度预言的器件，下面我们也尝试“预言”一番。

一、电路理论完备性

已知四个基本电学量：电流$I$、电压$V$、电荷$Q$和磁通量$\varphi$。从中任取两个量，就有$C_4^2=6$种组合，即六种关系：

$$ \begin{cases} R=\frac{V}{I} \\ I=\frac{dQ}{dt}\\ V= \frac{d\varphi}{dt}\\ L= \frac{V}{dI/dt}=\frac{d\varphi}{dI}\\ C= \frac{Q}{V}\\ \frac{d\varphi}{dQ}=? \end{cases} $$ 可以简单用下面的图表示： 

如果磁通量和电荷量存在一一对应关系，那么可以定义$\varphi$随Q的变化率:

$$ M=\frac{d\varphi}{dQ}=\frac{d\varphi/dt}{dQ/dt}=\frac{V}{I} $$ 即M具有电阻的量纲，但它的的值依赖于过去流经该器件的电荷总量Q，因此具有记忆功能。 ## 二、真实器件 2008年，惠普实验室发现$Pt/TiO_2/Pt$三明治叠层架构重现捏滞回线，并用简洁的边界迁移模型来解释器件的忆阻现象：电阻为$TiO_2$薄膜，由高浓度掺杂的低电阻($R_{ON}$)和低浓度掺杂的高电阻($R_{OFF}$)串联而成，电荷Q的积累会改变分配的比例，如图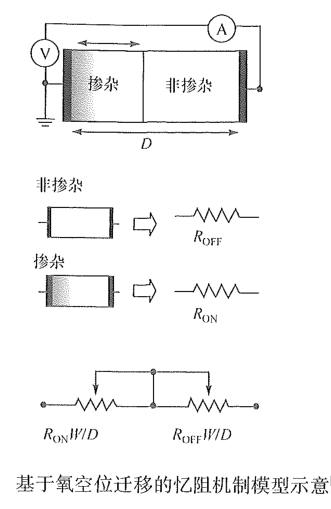：  数学关系描述如下： $$ \begin{cases} V=M(x)I \\ M(x)=R_{ON}x+R_{OFF}(1-x)\\ dx/dt=kI \end{cases} $$ 这里的x具有电荷的量纲，表示系统的状态变量。

三、数值分析

假设系统的输入电流$I(t)=I_0sin(\omega t)$，初始条件$x(0)=c$，可以积分得到状态变量：

$$ x(t)=c+\frac{kI_0}{\omega}[1-cos(\omega t)] $$

进而得到输出电压：

$$ v(t)=a_1sin(\omega t)+a_2 sin(2\omega t) $$ 其中$a_1 = (R_{ON}-R_{OFF})I_0(c+\frac{kI_0}{\omega})$，$ a_2 = (R_{ON}-R_{OFF})\frac{kI_0^2}{2\omega}$

选择参数$k=1\times 10^4,R_{ON}=100\Omega,R_{OFF}=10k\Omega,c=0,\omega=5rad/s$，利用matlab可以计算得到电压随电流变化的数值关系：(代码见附录) 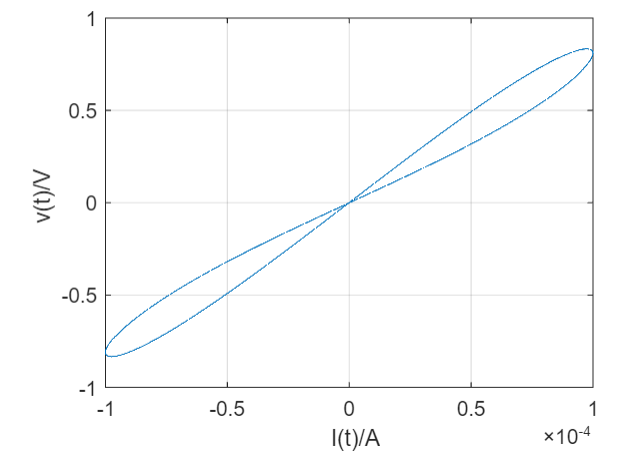与普通电阻的直线相比，忆阻器的电阻与“过去”有关，各点的阻值是该点与原点构造直线的斜率（不是切线斜率）。

再仔细比较电流$I$，状态参数$x$，电阻$M$，电压$V$随时间t的变化关系，如下：

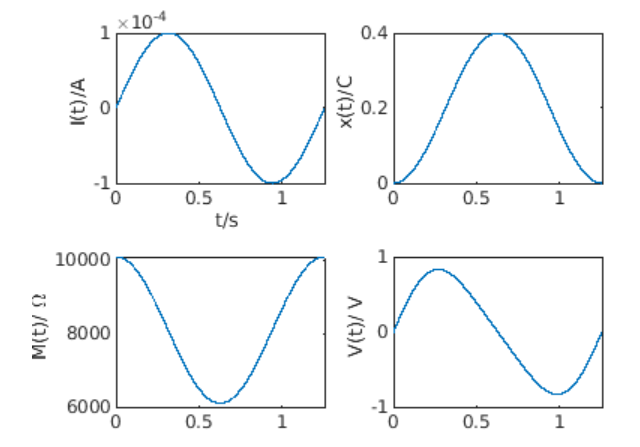
着重比较电流和电阻变化图，发现电阻在$6k\Omega$与$10k\Omega$之间波动，而且当电荷累积最大的时候，电阻达到最小值；无电荷累积的时候，电阻最大。

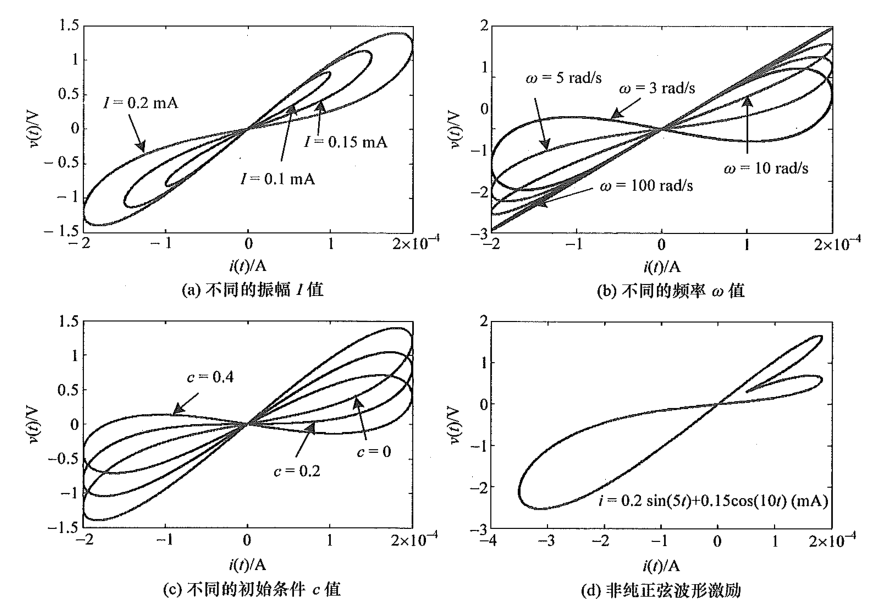
我们还可以变化参数，得到不同的电压——电流变化图：

附录

% 1.basic parameter
clear;clc;
k0=1*10^4;
R1 = 100;R2 = 10000;
% I = 0.1,0.15,0.2mA
I = 1*10^(-4);
% w = 5, 3,10,100rad/s
w = 5;   
% c = 0 , 0.2, 0.4 
c = 0;
% 2.time
delta = 0.0001; t = [0:delta:2*pi/w];
%% 3. it,x,M,V
it = I*sin(w*t);
%it = 2*I*sin(w*t)+1.5*I*cos(2*w*t);
N = size(t);N = N(2);
intit=it;
for k=2:N
    intit(k)=it(k)+intit(k-1);
end
intit = delta *intit;
x = c+k0*intit;
M = R1 + R2*(1-x);
V = M.*it;
plot(it,V);
%% show result
subplot(2,2,1);plot(t,it);
subplot(2,2,2);plot(t,x);
subplot(2,2,3);plot(t,M);
subplot(2,2,4);plot(t,V);

顺便推荐matlab在线运行的网址，只需要学生邮箱注册。