量子霍尔效应
一、什么是霍尔效应
如图，如果在垂直于电流的平面上加上磁场B，那么载流子（可以是电子，也可以是空穴）会往两边堆积，在纵向形成电场，用来平衡运动电荷在磁场中的洛伦兹力，稳定时，两边的电压为$V_H$，这时载流子收到的洛伦兹力和侧向电场力平衡，载流子不偏转，稳定朝电流方向运动。
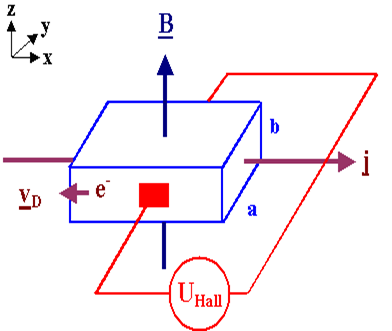我们来具体计算这个侧向电势大小。定性来看磁场越大，电流越大，两侧的电势就越大：
实验时，可以改变磁场强度和电荷密度来观察霍尔电势$U_{Hall}$的变化。
正常的霍尔效应是，当增大磁场时，其对载流子的偏转增大，霍尔电势增大；当增大电荷面密度时，相等电流下，偏移速度减小，受磁场偏转小，霍尔电势减小。
二、量子霍尔效应的实验
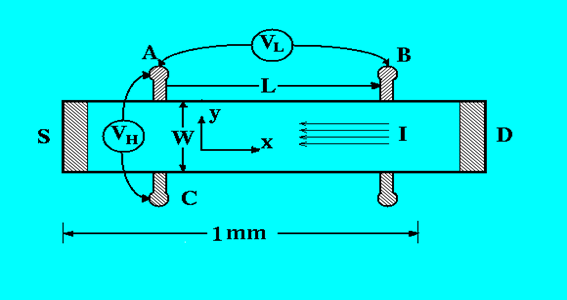让我们看看量子霍尔效应是怎么发生的，如图是MOS管的俯视图，S是源极，D是漏极，栅极G(未画出)垂直于平面，隔着一层二氧化硅电容，增加G的电压就可以增大载流子面密度$n_s$，AC两端的电压$V_H$就是霍尔电压，AB两端的电压$V_L$是普通的电压降，电流$I$和$V_g$不变时，它也不变。
1、二维平面
这里以NMOS管为例，导电的载流子为电子，用MOS管的好处是，和一般电阻导电不同，它的反型电子刚好约束是在薄薄的二维平面运动，这个特性能够更容易观察到量子效应的发生。
实验需要在极低温度下进行，一般是液氦4.2K，因为这样可以大大减小粒子的热运动。同时磁场强度达到了$19.8T$，要知道地磁场的强度约为$50\mu T$，一般磁铁的磁场强度为$0.5T$。在这种情况下，我们可以得到如下实验结果：
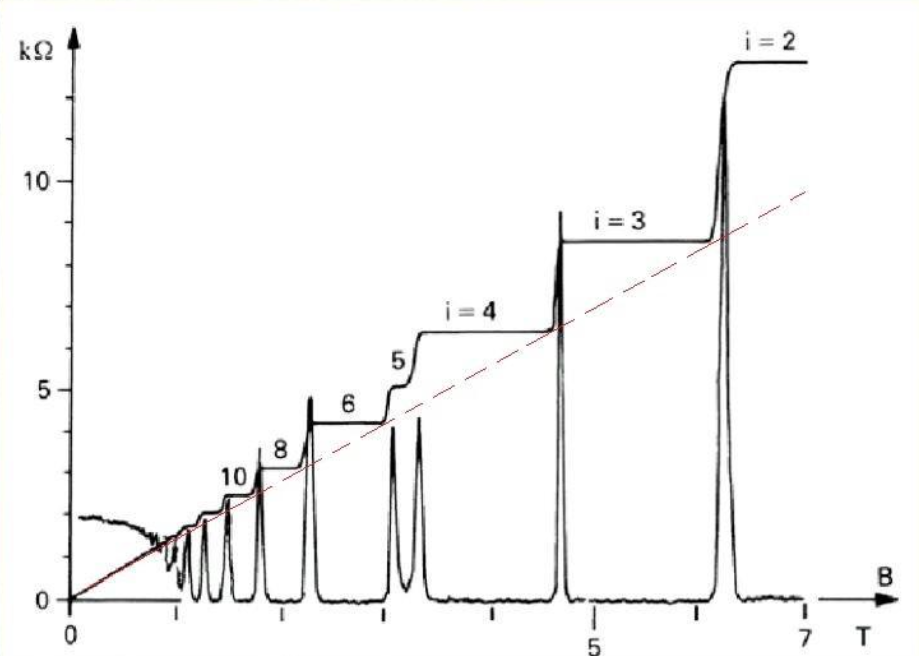横坐标自变量为磁场强度B，图中的虚线表示：如果没有量子效应，霍尔电阻的变化曲线。有平台的实线表示实际的霍尔电阻曲线，上面的序数$i$表示的量子数，后面会详细解释。而带尖的曲线表示电流方向上的电压降或电阻。可以看出，但霍尔电阻(或电压)出现平台时，电流方向上的压降为零，也就是电阻为零！而霍尔电阻不再呈线性变化。
2、如何控制电流、电子面密度
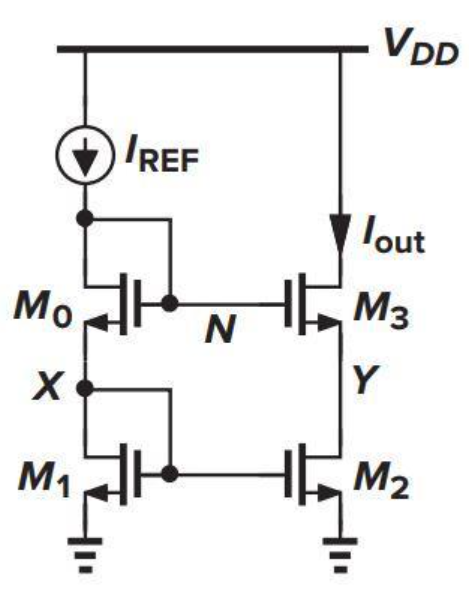
上图是电流源产生的一种方式，图片来自于拉扎维的模拟集成电路，偏置电流$I_{REF}$可以很容易由$M_0 M_1$确定，输出电流$I_{out}$基本上可以看成是恒流源，$M_3$和$V_{DD}$之间接上待测原件即可。
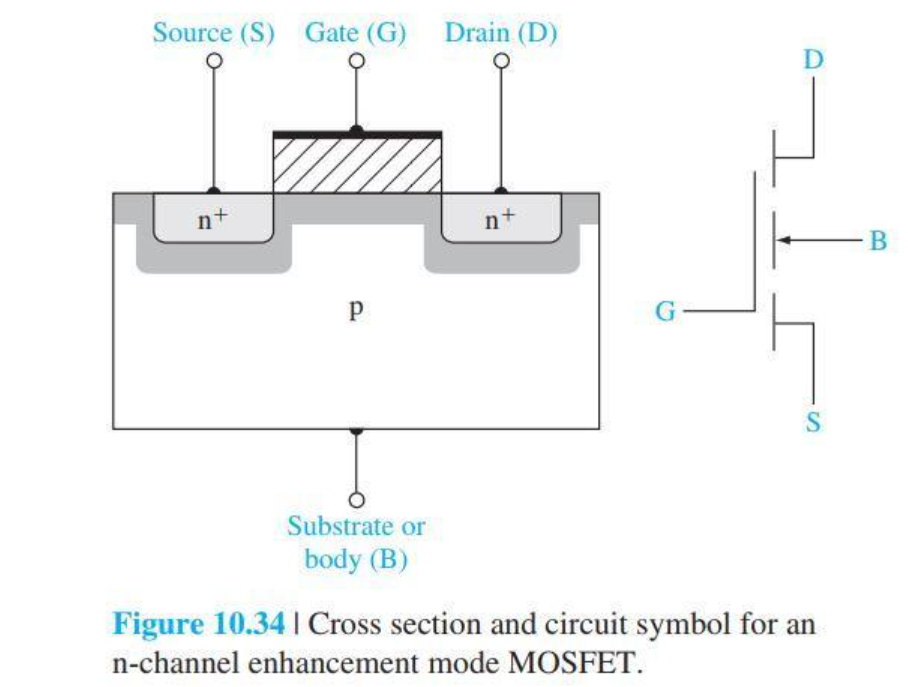
上图是增强型NMOS管的侧视图，图片来自于尼曼的半导体物理与器件(是一本不可多得的好书)。MOS管的另一个好处是，栅极G可以控制电子强反型的程度，进而控制电子面密度：
$$ n_s=C_{ox}*(V_{gs}-V_t) $$ 这里的$C_{ox}$为二氧化硅层的电容，$V_{gs}$为栅源的电势差，$V_t$是MOS管的阈值电压。容易看出，只要改变栅电压，就可以相应改变电子面密度。实验结果如下：
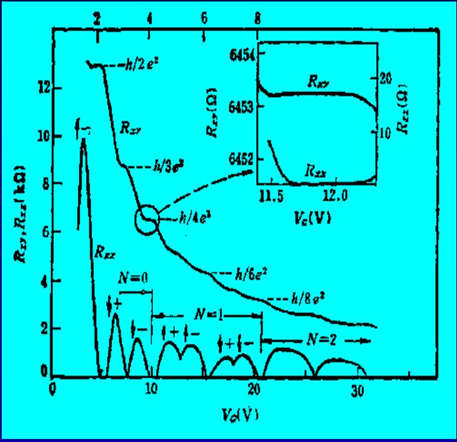
横坐标为自变量是栅源电压，当它逐渐减小时，可以发现霍尔电阻$R_{xy}$的平台越明显，平台下对应的水平电阻$R_{xx}$为0。可以看出本该与$n_s$成反比的$R_{xy}$，现在出现平台，而且平台电阻的数值仅和普朗克常数和电荷常数有关，与材料，电压，磁场等无关！
那么我们来重点关注实验一：
- 为什么霍尔电阻$R_{xy}$会出现平台？
- 为什么水平电阻$R_{xx}$会有出现零的状态？
- 电子在平台期间呈现什么奇特的运动状态？
三、直观物理图像
为了更加直观地了解这一现象，我们先不直接上薛定谔方程，试试用经典的图像来分析这一现象，也便于和之前的推导比较。
1、磁场下的圆周运动
先假设没有水平电流的情况，如果此时加入磁场，由于电子本身有热运动的速度，那么它会在磁场的作用下做圆周运动：
$$ m\frac{v^2}{r} = qvB\Rightarrow r=\frac{mv}{Bq} $$ 接下来就要引入量子效应了，假设电子绕一周必须满足波长的整数倍(经典方法推导氢原子能级分裂时也用到这种思想)，那么这样就会对其速度或能量有约束： $$ 2\pi r=N\lambda=N\frac{h}{mv}\Rightarrow mv^2=N\hbar \omega,N=1,2,3... $$ $\omega \equiv \frac{Bq}{m},\hbar \equiv \frac{h}{2\pi}$可以看出，量子化后的电子呈现分立能级，那么每一个能级能容纳多少电子呢？这就是能级的简并度，类似一层楼能容纳多少人。2、二维平面的能量密度
现在考虑无磁场，无电流时的二维平面自由电子气，设其长宽为L、W，波矢$\kappa$也要量子化：
$$ \vec{ \kappa} = \frac{2 \pi}{W}\vec{i}+\frac{2 \pi}{L}\vec{j} $$ 波矢和能量关系： $$ E= \frac{ \hbar^2 \kappa^2}{2m} $$ 能量密度： $$ G(E)dE=G(\kappa)d\kappa=\frac{2\pi \kappa d\kappa}{2 \pi/W *2 \pi/L} $$ 单位面积态密度： $$ g(E)=\frac{G(E)}{WL}=\frac{2\pi \kappa }{2 \pi *2 \pi} \frac{1}{dE/d\kappa}=\frac{m}{2 \pi \hbar^2} $$ ### 3、霍尔电阻量子化 二维电子气的一个特点是，它的单位面积态密度与能量大小无关，由第一部分知道电子能级差为$\hbar \omega$，第二部分知道单位能量的状态密度为$g(E)=\frac{m}{2 \pi \hbar^2}$，因此能级简并度即为两者乘积： $$ g(E)*\hbar \omega=\frac{m}{2 \pi \hbar^2} *\hbar \frac{Bq}{m}=\frac{Bq}{h} $$ 这说明什么呢？电子只能处于分立的能级，每个能级的电子数为$\frac{ Bq}{h}$，假设由$i$个能级填满，那么$n_s=i*\frac{ Bq}{h}$，带入： $$ R_H\equiv \frac{B}{n_sq} =\frac{h}{i*q^2}=\frac{25.8 k\Omega}{i} $$ 这里的$i$就是“实验一”中的量子数。 ### 4、详细的过程分析 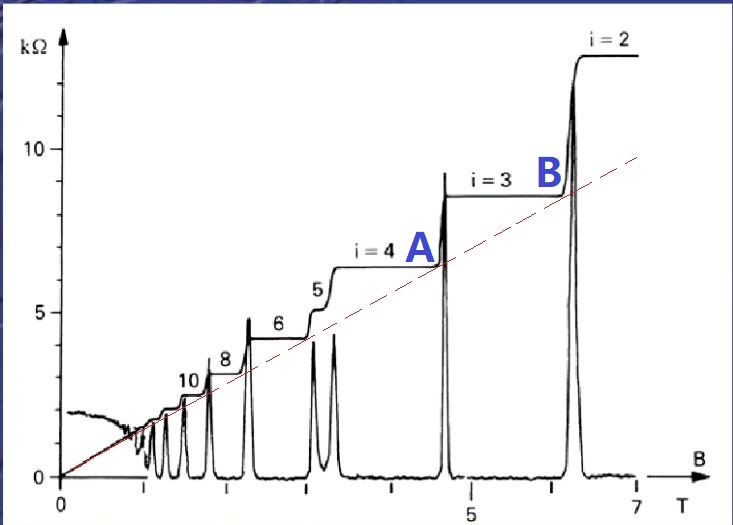 假设此时磁场加在A的位置，这时电子占满了四个能级，总的电子面密度和不考虑量子效应时相等(A点也在红色虚线上)，这时，加大磁场，能级简并度$\frac {Bq}{h}$增大，总电子数占满了前三个能级后，占不满第四个能级，这些“多余”的电子被挤向了“局域态”，它是由缺陷导致的，好像电子被束缚在原子核周围，这些电子不参与导电，这样参与导电的电子突然减少，就会导致图中霍尔电阻的徒然上升。当磁场继续增大，能级的“容量”增大，原来局域态的电子会部分填满能级，因为填满后的电子数正比于磁场强度，所以相除之后，霍尔电阻不变，于是出现了稳定的平台。那么为什么水平电阻此时为0呢？
因为基态和激发态之间存在能隙，在极低温度下，电子既不能获得足够能量跃迁，又不能前往已经占满的低能态，无处可去的电子只能挤在一起，形成所谓的超流，它们步调已知，不会受到散射，故不需要额外的电场驱动就能维持电流，类似于光滑平面的匀速运动，所以水平电阻$R_{xx}=0$
当磁场继续增大至图中B点，局域态中的电子已经完全进入前三个能级上，此时的霍尔电阻又和经典情况一样，继续增加磁场，超流态破坏，部分电子又变成局域态，会有强烈散射，水平方向的电阻又不为0，出现一个峰值。
四、量子力学理论解释
经典的推导方式有许多不严谨的地方，比如态密度的推导在没加磁场和电流的情况，能级分裂又在没电流的情况推导。量子力学则直接在磁场和电场条件下，求解薛定谔方程，求解的波函数显示，电子一方面在水平方向呈现平面波(简单理解为匀速运动)，另一方面在垂直方向做谐振(对应经典图像里的圆周运动)，谐振频率为$\omega=\frac{Bq}{m}$，而且谐振能级是分裂的，能级差为$\hbar \omega$。
但经典的图像比较直观，有助于理解电子“品性”。
五、其他
1、霍尔电阻平台的平整度极高，误差为$10^{-8}$，这一特性被用来制定电阻标准。 2、整数霍尔效应之后两年，崔琦等科学家又发现了分数量子霍尔效应，并提出了新的物理图像来解释这一现象。 3、2018年复旦大学的修发贤组在砷化镉材料中发现三维空间的量子霍尔效应。 4、2006年，斯坦福大学张首晟团队提出了量子自旋霍尔效应的理论，意在利用电子自旋和电力的规律，降低能耗，研制新型计算机，并在2009年预言了三种拓扑绝缘体。 5、2013年，清华薛琪坤团队在实验上观测到量子反常霍尔效应，它不同于之前的量子霍尔效应，它不依赖于强磁场而是由材料本身的自发磁化产生，在零磁场下就能实现，不过仍需要低温环境。